ahuranga.com > 2D Illustrator > wavelets
Wavelets
Tools used: Matlab, Python
Wavelets are a relatively new discovery. They have many similarities to Fourier transforms, but unfortunately were studied too late to be a full replacement. Much like Fourier transforms we can shift from the frequency domain to the time domain and vice versa.
Perhaps the most promising application is in the field of image compression. JPEG while being much more popular, has a great deal of draw backs. JPEG compression divides an image into 8x8 pixel squares where a discrete cosine transform (DCT) is applied to each square. The image is then converted and represented as a series of 64 functions. These 64 functions are shown below:
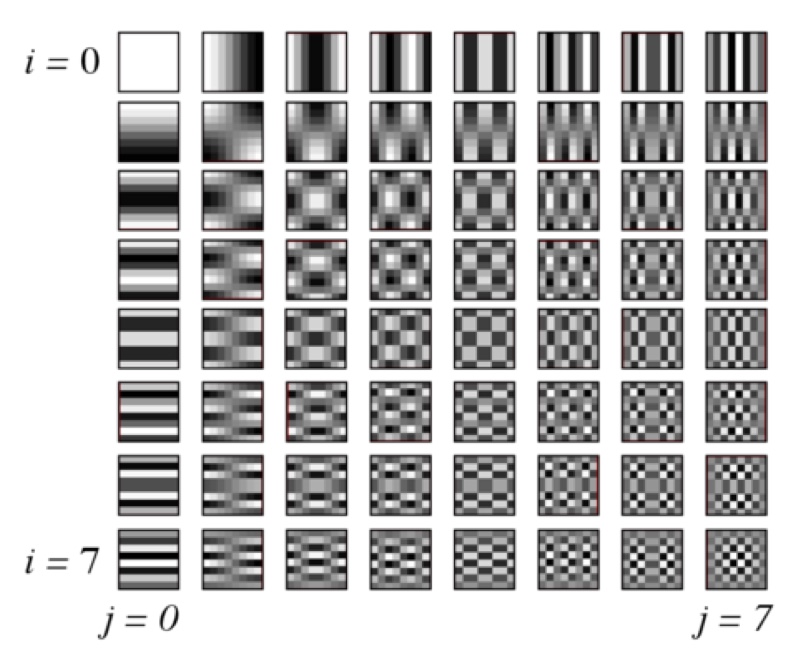
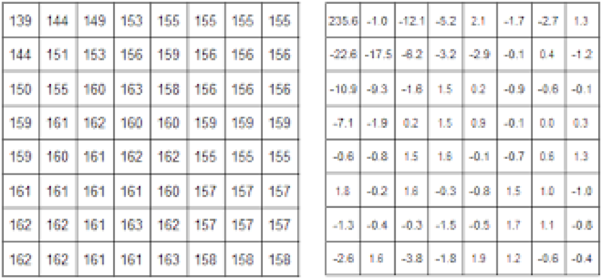
An 8x8 block would then be represented by an 8x8 matrix of how much the block corresponds to each function. For example, a completely white block would be a matrix with 255 in the top left corner and zeros everywhere else. Mathematically you are more likely to have high (absolute value) numbers for the top left functions and low numbers for the bottom right functions. Below is an example. The numbers on the left correspond to the pixel values of an 8x8 block. 255 is white while 0 is black. On the right is the corresponding DCT values.
When you ignore the smallest values, you have a similar but compressed image. The main problem with this process is that JPEG tends to leave artifacts, especially around text. Looking at the 64 basis functions I mentioned above you can see where these artifacts come from.
Wavelets are important because they do not have these problems.
In the top right corner is an example of an image that has been transformed one level using DWT. The great thing about this process is that you use a wavelet signal to extract certain frequencies that our exes cannot pick up very well. The result is an image with one quarter the resolution but with very similar quality. The concept of Multi resolution analysis allows us to go another level and extract more information for an image one eigth the original with similar quality.
Extracting unwanted information also has applications to the fields of computer vision and edge detection. Ultimately, the “unwanted” information are areas of high frequency changes. Many times this corresponds to the edge of an object. In the robot project I used this property to find the outlines in an image to assist artists when drawing murals.
