Calculating 100yr return period using python
I have always loved working with numbers and I have always been fascinated with hydrology. This project started as an opportunity to combine these two interests (plus it allowed me to improve my Python skills!). I started with some rainfall data in a csv file. It contained almost daily rainfall numbers over a period of 40 years. I started with almost 15,000 data points, and I wanted to see if I could clean the data up a bit.
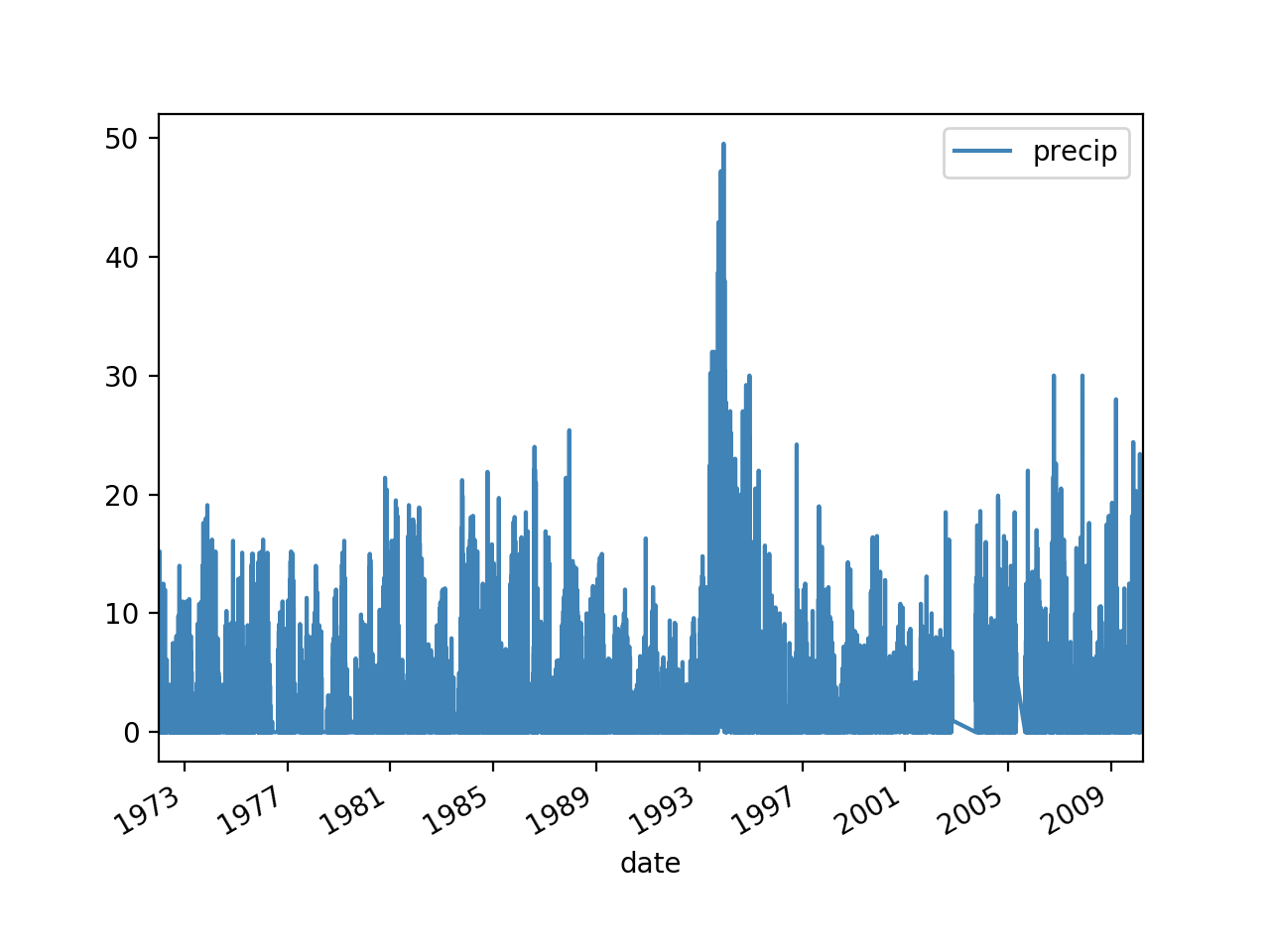
Original 40 year daily rainfall data
The first step was to find the maximum annual rainfall for every year available. The problem was combing through the daily data values most of which were 0mm. Once I had the maximum annual rainfall I could begin determining the normal distribution. The first thing I did was to parse the csv information. This involved importing the file, extracting the date, separating the date into year, month and date. I only really cared about the year. Once these were separated, it was simple to determine the yearly maximum, and create a new csv with only the annual maximum. The new graph is below:
It was important to extract the maximum from the rest of the data since the lower values affect the return period and we are more concerned about the peak annual rainfall. With this new set of data I then calculate the mean and the standard deviation. With these numbers, I can determine the normal distribution of the data. Below is a plot of the number of years with a given peak rainfall in mm, overlaid with the normal distribution.
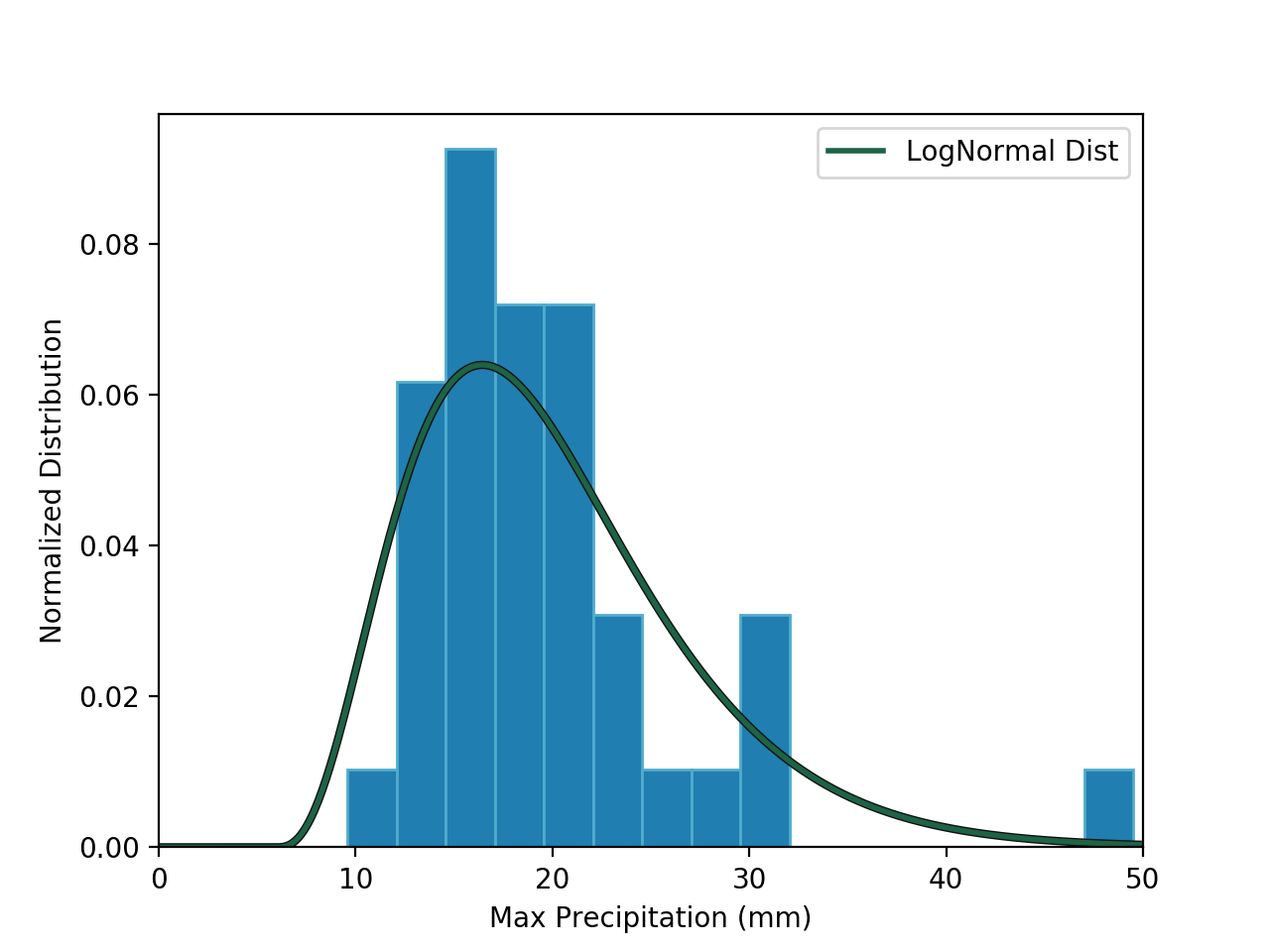
Log-Normal Distribution
The 100 year storm is determined to produce 41.1mm in rainfall. Python is great for probability analysis since scipy comes with many probability tools. To determine the 1% storm, I only need one line of code:
p100y_lognorm = stats.pearson3.ppf([0.99], skew=1, loc=mean, scale=stdDev)
There is still much more I can do, but it was a great learning experience. I learned a lot about working with csv in python, and there is still so much more to learn.
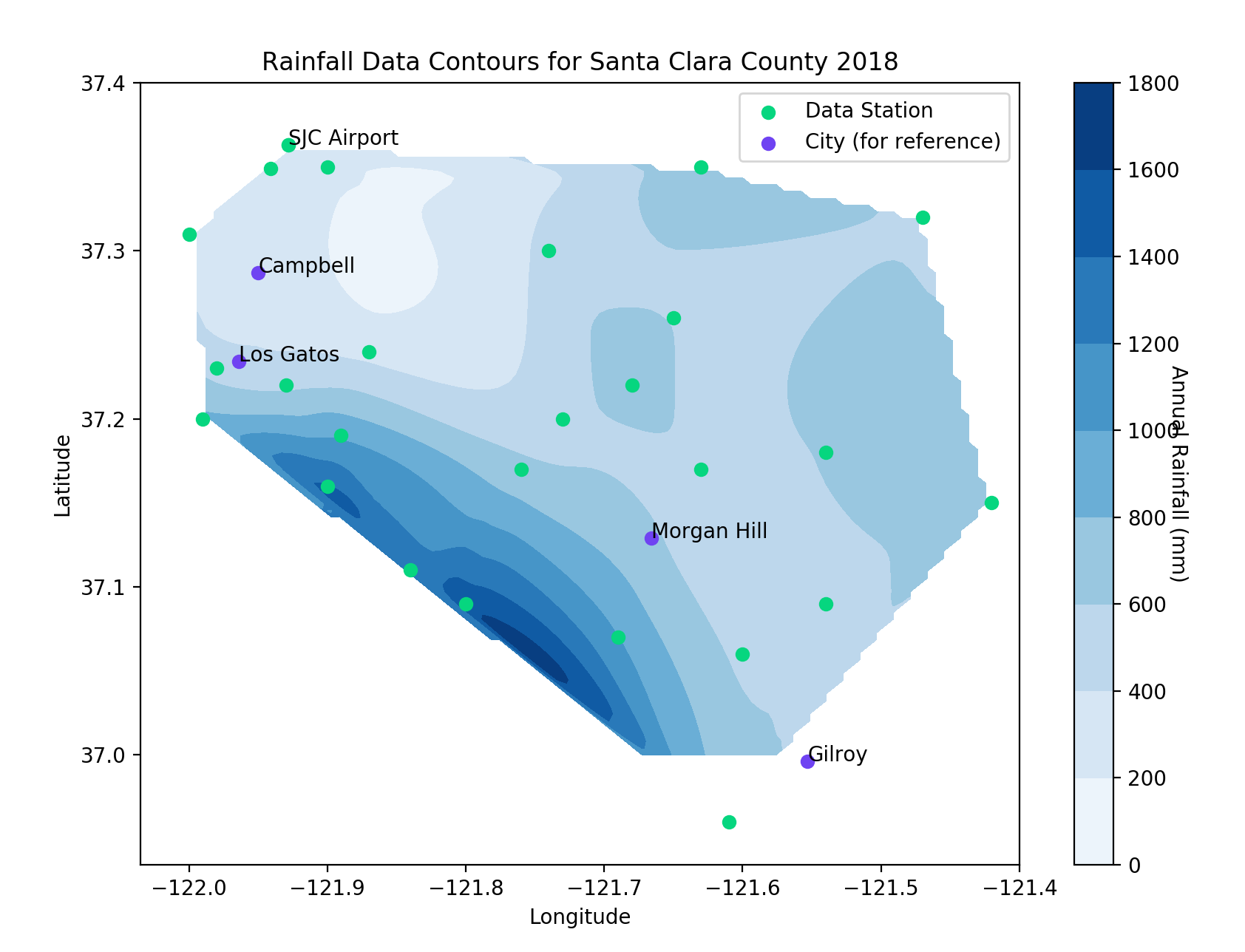
Visualization of Santa Clara County Rainfall Data
This project is similar to a problem I encountered at work. The storm drains in the eastern portion of a town were always over capacity during storms. I had to investigate possible explanations and to research solutions. Since this was a rural area, there was no IDF curves I could work with. What I did have was historical rainfall data from a variety of stations. The first step in this project was to map the data so we could gain a better understanding of the site.
Rain guage locations
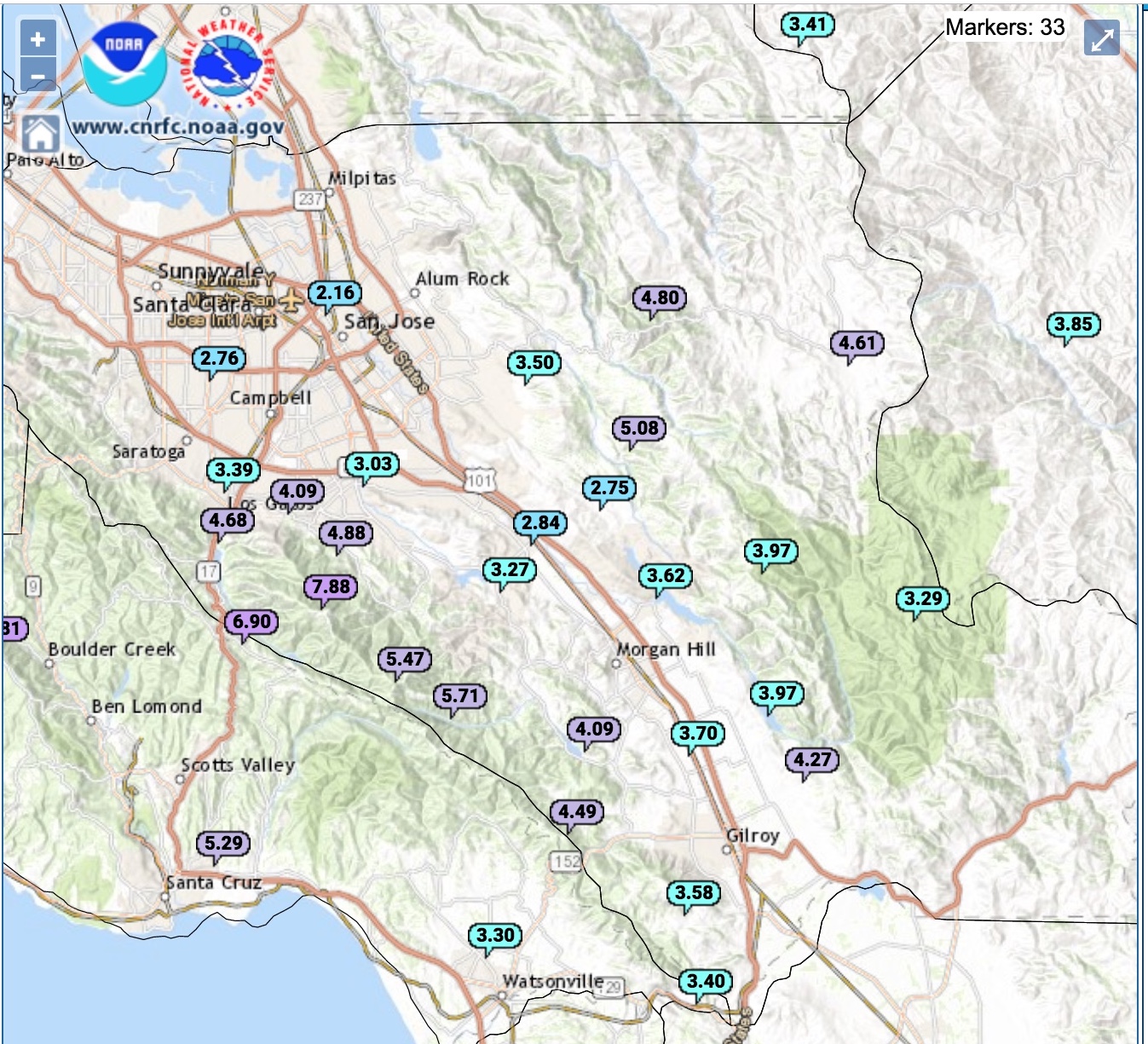
I wanted to recreate this project using weather data from Santa Clara County. Above are the locations of the stations with the most recent monthly rainfall in inches. I used the NOAA website to find the data for the total yearly rainfall, extracted only the stations in Santa Clara County, and created a contour map. The figure is below:
As you can see the highest rainfall occurs near the Lexington Hills area which makes sense since it corresponds to the area with the highest elevation. I did discover a potential issue with the figure, there is a section with shows close to 0mm precipitation when there is no information or data points that would lead to that result.
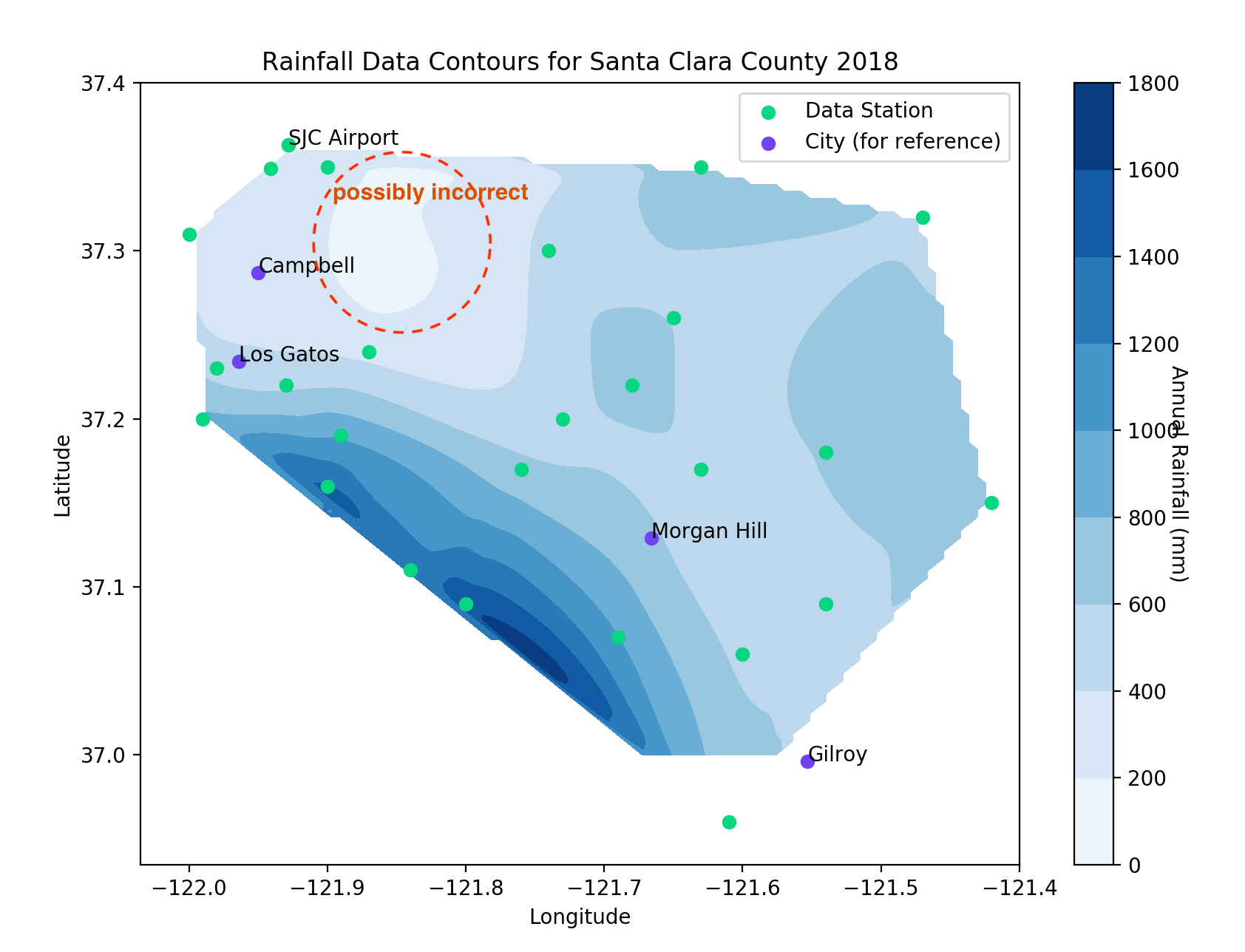
Possible error
After reading the Scipy documentation I think I know why. Scipy uses cubic interpolation. Cubic is usually great for modeling terrain, although it has problems interpolating flat areas, especially if two points are flat and then the third points is a huge jump (perhaps my next project can be on interpolation techniques). Below is a quick example. If I were modeling the topology, that dip might be accurate, in this case it probably is not accurate. I will continue to read the documentation and repeat the model and see if there is a change in the results.
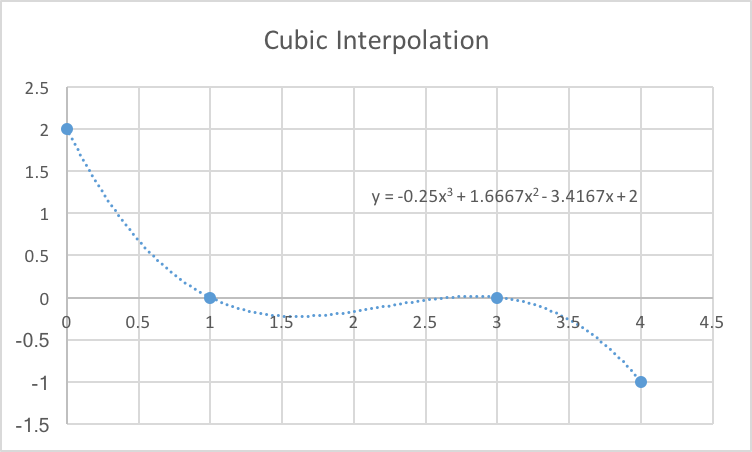
Simple cubic interpolation example
Pipe Friction solver in Python
Background
This project started as a thought I had during my first course in water resources. I always wondered if there was a way to solve the friction formula without having to use the moody diagram. Don’t get me wrong, being able to read the Moody diagram is very important, but this method is not very accurate and can be confusing which can lead to errors. The problem with solving the problem implicitly is that you have the friction factor on both sides, and one is in a log function, which makes factoring difficult.
Instead, it is much easier to solve the equation numerically. As shown below.
How it works:
I created a python script which can return the friction factor. It is not perfect and I am still testing different input methods. The way it works is simple, it asks you for different values such as the flow velocity and pipe thickness and returns other coefficients as it solves them. It returns the Reynolds number and the friction.
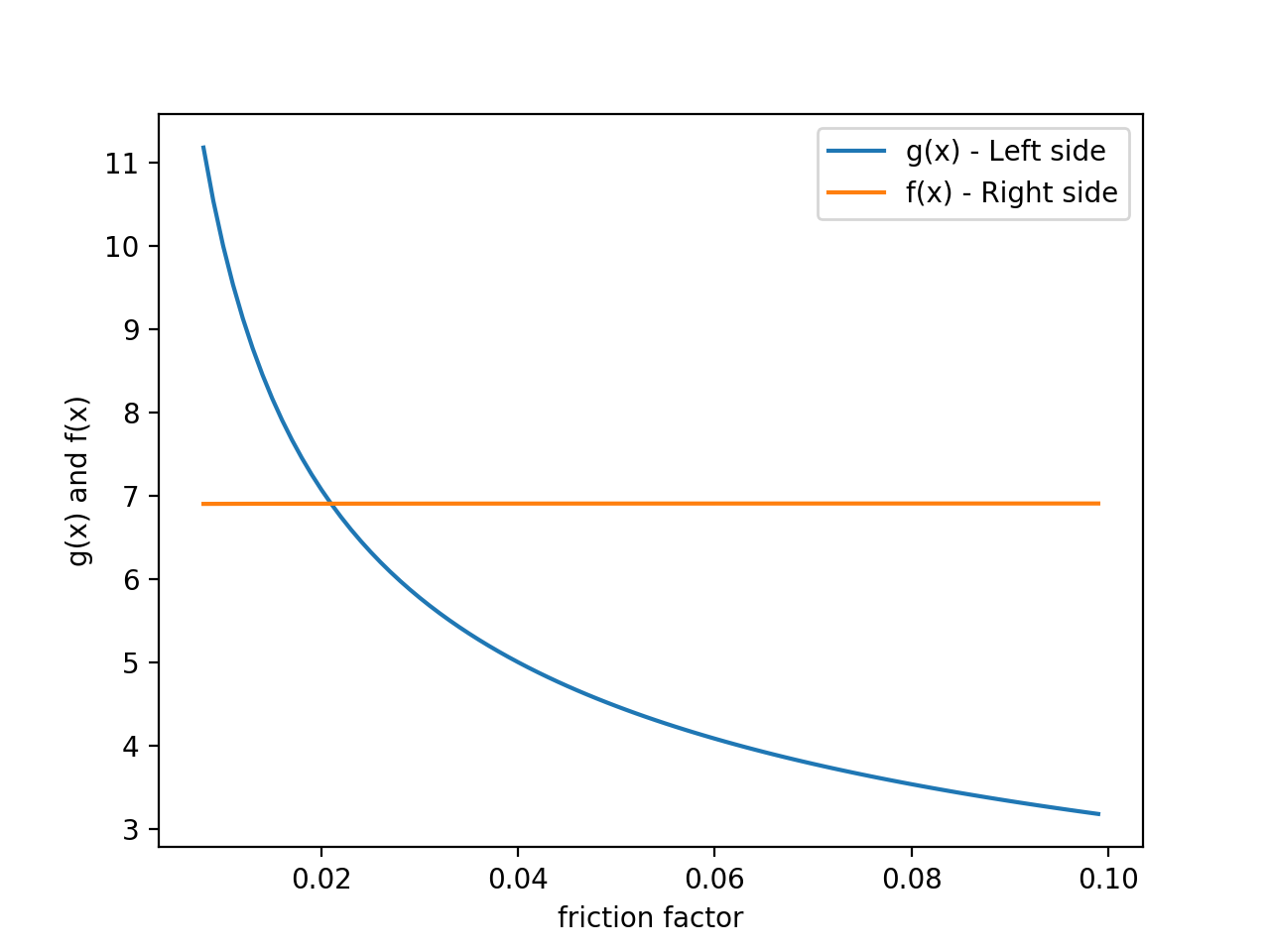
Plot of both sides of Colebrook–White equation
If you consider the left side of the equation to be g(x) and the right side to be f(x) you can set g(x)-f(x) = 0 ; plot the function and find the root of the equation. As I mentioned earlier, having a factor inside a log function makes factoring difficult, instead I use the false position method to find an approximate root numerically.
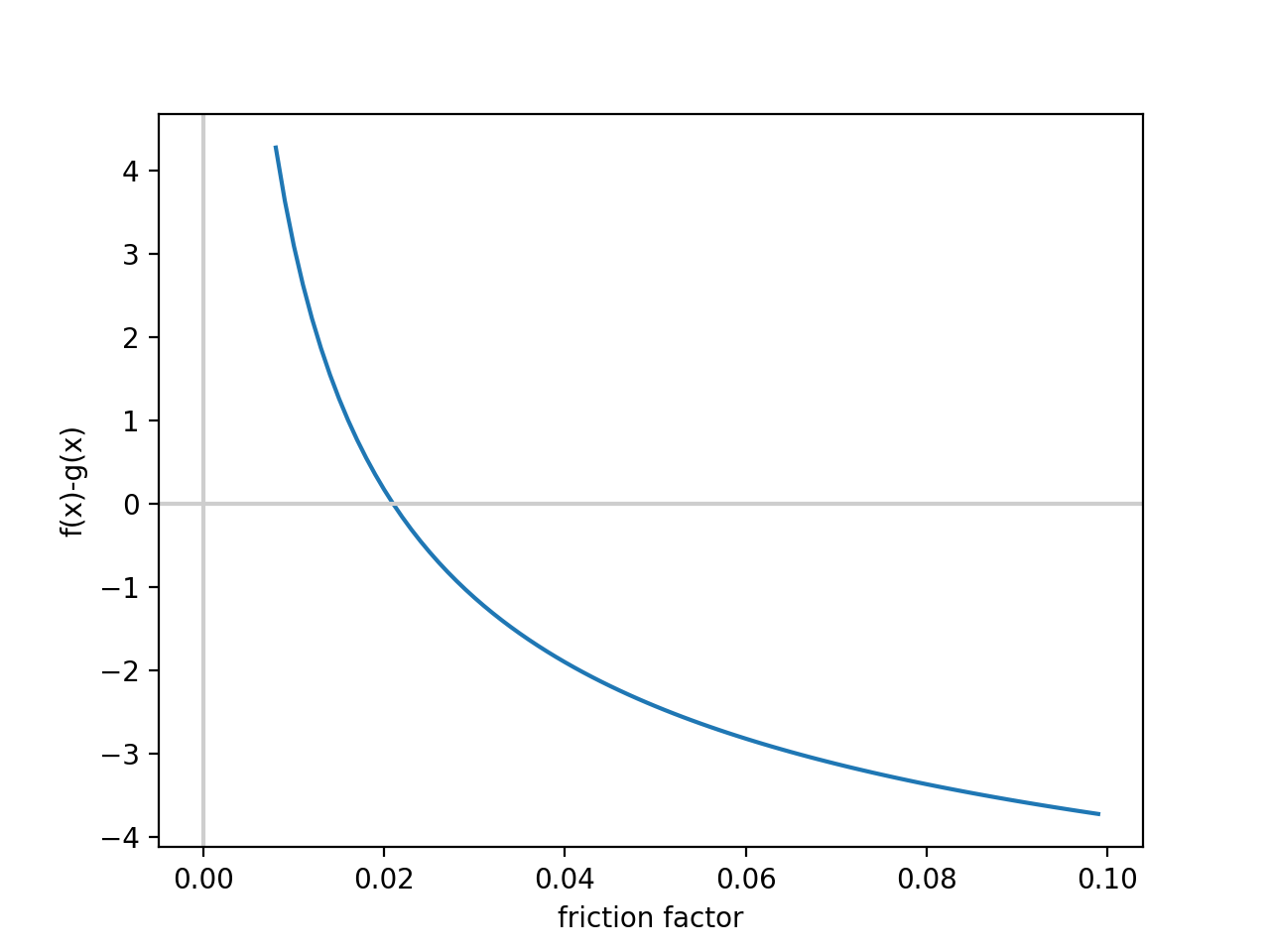
Plot of : h(x) = g(x)-f(x) = 0
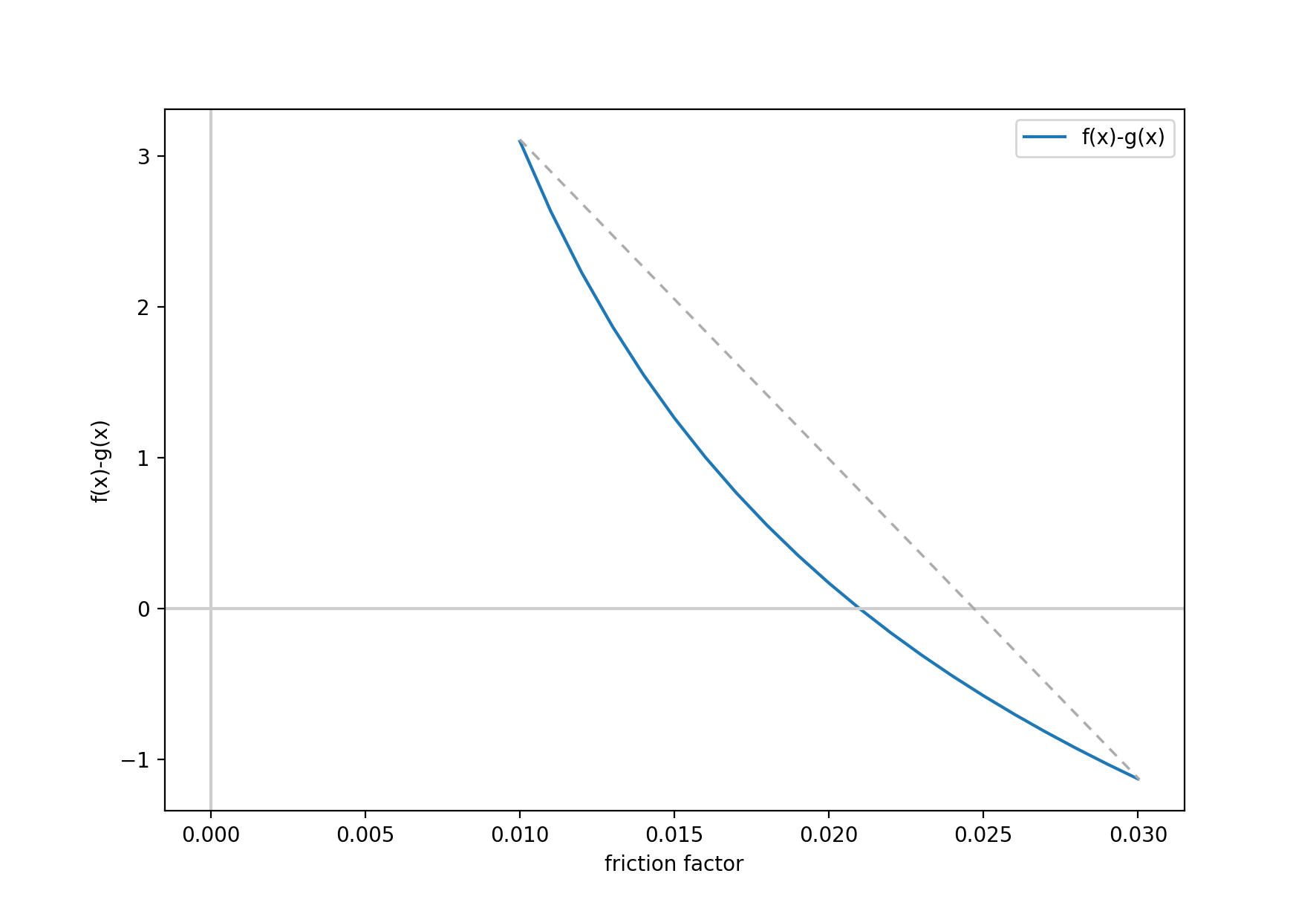
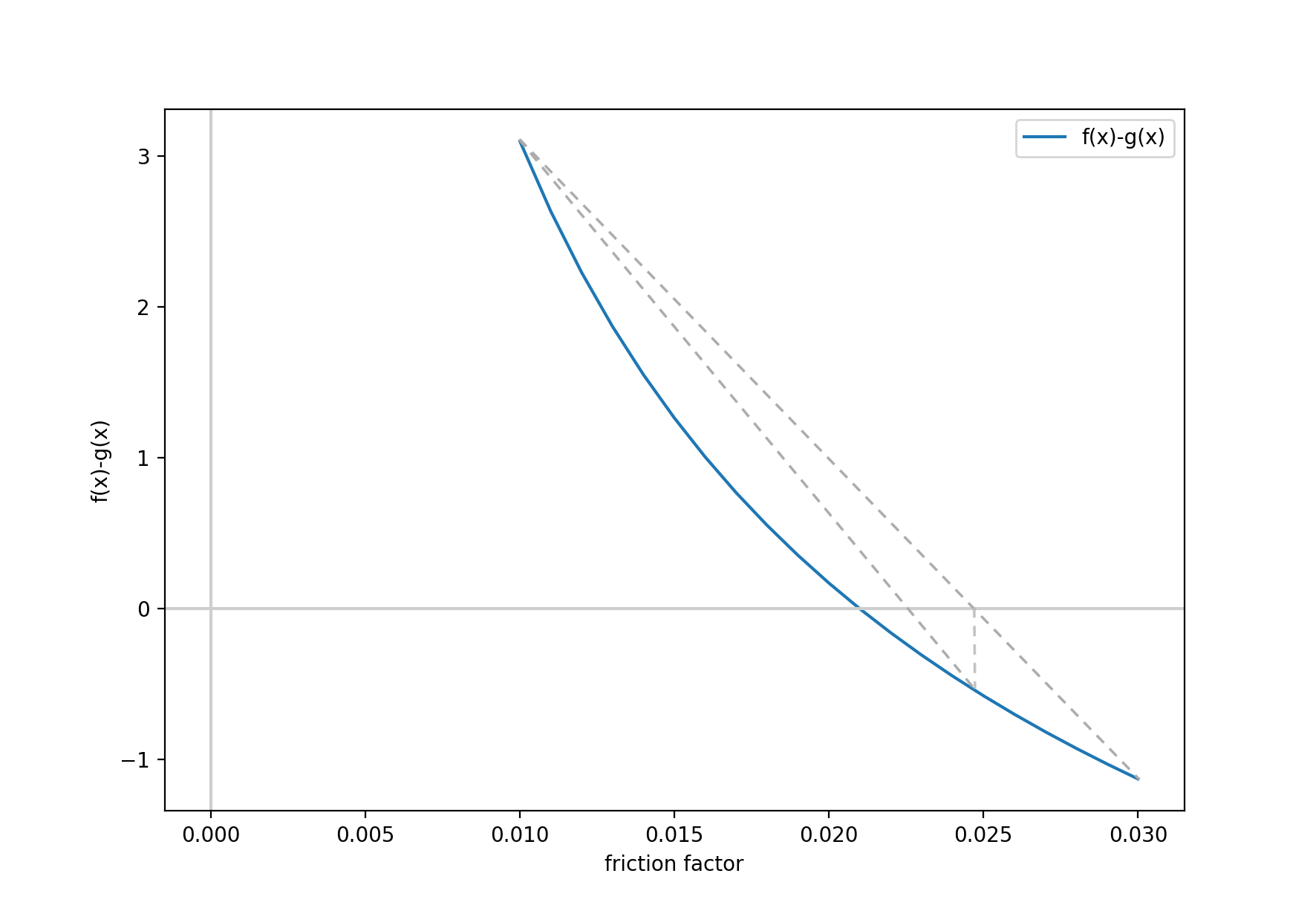
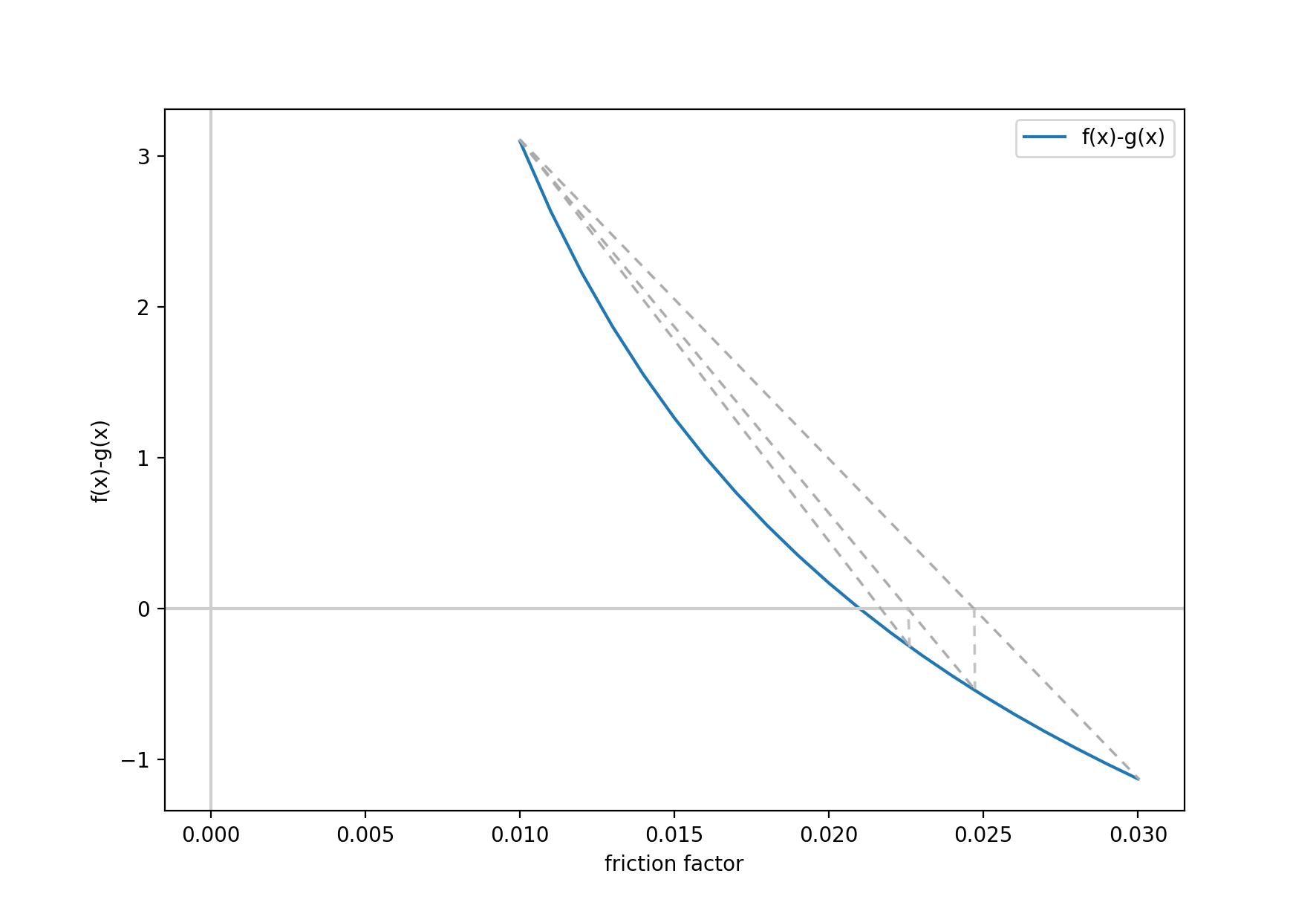
The process is as follows. First it solves the g(x)-f(x) using increasing sample points for x, until the sign changes. Once the sign changes, then you have your bounds. In this example, the sign changed around x = 0.022, and the bounds were set to [0.01,0.03]. First you draw a straight line from h(0.01) to h(0.03) and find where it crosses the x axis, this is your new x, in this case ~0.0255 and the new bound becomes [0.01,0.0255], and you repeat the process until h(x) = 0 ± 0.0001.
Below is a graphical representation of the false position method:
The output is below. Everything that starts with the word “What” requires user input, everything else is the result of the calculations.
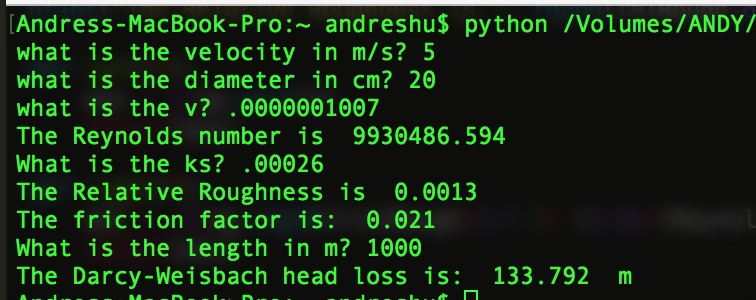
The false position method results in a friction factor of 0.021 which is the same if you were to use the Moody Diagram, but the process is faster and much simpler.
Next steps
I am still working on this, the goal is to have a GUI that gives the user more flexibility. For example if you know the Reynolds number but not the velocity, and this current configration expects a very rigid set of inputs.
Watershed Runoff Calculation
I started working on this while I was studying for the P.E. exam. I found a problem in an old textbook where you are given the precipitation data and the infiltration rate. It asks to determine the runoff in cfs. These calculations are important since as you see in the results, the peak flow occurs well after the storm itself has ended.
Once you have the hydrograph, it is a simple algorithm to calculate the discharge for each hour. Naturally I wanted to calculate everything in python. The resulting table is below:
[[ 5. 0. 0. 0. 0. ] [ 17.5 20. 0. 0. 0. ] [ 42.5 70. 40. 0. 0. ] [ 30. 170. 140. 36. 0. ] [ 5. 120. 340. 126. 30. ] [ 20. 105. 306. 240. 20. ] [ 15. 70. 255. 216. 40. ] [ 10. 52.5 170. 180. 36. ] [ 0. 35. 127.5 120. 30. ] [ 0. 0. 85. 90. 20. ] [ 0. 0. 0. 60. 15. ] [ 0. 0. 0. 0. 10. ]]
Each row represents an hour in time and each column represents that hour’s rainfall contribution to the discharge. You simply add all the values in each row and you get the total runoff for that hour. The results are:
[ 5. 37.5 152.5 376. 621. 691. 596. 448.5 312.5 195. 75. 10. ]
The final plot: